心臓の活性化理論と心不全■ １０.心筋連結橋回転エネルギ－

2014年1月1日竹田幸一心臓の活性化理論と心不全

■ １０.心筋連結橋回転エネルギ－

10.1 連結橋の「エネルギー張力変換効率(f/eA)」

心臓収縮にともなうエネルギー消費のメカニズムは心臓力学とともに心臓生理学上のもう一つの主要なテーマである。心臓の消費エネルギーが心筋の発生張力や心臓のする仕事量とどの様に関連するかは，それ自身，大変興味深い問題である。さらにこの関係は心不全や虚血性心疾患の重要な治療目標である心筋のエネルギー効率改善という観点からも実際問題として重要である。消費エネルギーは心筋標本では発生熱量を，in vivo心臓では冠動静脈血中の酸素分圧較差から計算した酸素消費量(VO2)から推測することが可能である。これらの測定は必ずしも簡単ではないので，消費エネルギーを推測する代替の指標としての何かの機械的パラメーターが必要である。それらの理由から心臓の消費エネルギーと機械的パラメーターとの関連が詳しく調べられた。代表的な機械的パラメーターは，１）心筋への外的負荷(Fp)40, 74, 119)，２）心筋発生張力の時間積分値(force-time-integral: FTI)67, 144)，３）in vivo心臓では左室の圧ー容積面積(pressure-volume-area: PVA)152)である。心筋・心臓の全消費エネルギー(U)とFpまたはPVAとの関係はU-Fp平面，U-PVA平面においてほぼ直線関係となる。catecholamine投与9, 59, 157)や低温状態9, 111, 153)においてもこの直線関係のなす傾きは変化しないが，甲状腺機能異常では変化する63, 81, 112)。一方，全消費エネルギー(U)とFTIとの関係はU-Fp関係やU-PVA関係と同様にU-FTI平面においてやはり良い直線関係にあるが，前者と大きく異なるのはcatecholamine投与や低温状態においてこの関係の傾きは容易に変化することである3, 9)。しかも甲状腺機能低下ではU-Fp関係やU-PVA関係と同様に低下する81)。このようなU-Fp関係，U-PVA関係，U-FTI関係全ての近似的直線関係や，様々な干渉を与えた時の異なった反応の理由については現在までほとんど分かっていない57, 153)。

一個の活性連結橋が張力(f)を発生しながら単位時間連続して回転する時に消費するエネルギーをeAとすると，f/eAは回転する連結橋一個あたりの化学的エネルギーから機械的張力への「エネルギー張力変換比率（または効率）」を表す。この値の逆数(eA/f)はmyosin ATPaseのchemo-mechanical transduction活性と比例関係にある。連結橋一個あたりの発生張力はそれが総合されて心筋の発生張力となり，その心筋の短縮を通じて心臓のなす外的仕事に最終的に変換されてゆく。従って，連結橋一個あたりの「エネルギー張力変換比率」は最終的には心臓の仕事効率（心臓のした外的仕事量と全消費エネルギーの比）を確定する根本的数値の一つであり，心臓の「エネルギー変換効率」の最も基本的な指標とも考えられる。U-Fp関係，UFTI関係の傾きの逆数は心筋収縮に伴う全消費エネルギーに対する心筋発生張力（またはその時間積分値）に相当するので，これは心筋の「エネルギー張力変換比率」を表す指標である。一方，U-PVA関係の傾きの逆数については，PVAの中に心筋のした機械的な外的仕事量以外の非機械的な仕事量をも含んでいるので，U-Fp関係，U-FTI関係の傾きの逆数と同一には論じられない。U-Fp関係，U-PVA関係，UFTI関係の傾きの逆数が連結橋一個の「エネルギー張力変換比率」の指標であるf/eAとどの様な関係にあるかは未だ分かっていない。

もしU-Fp関係，U-PVA関係，U-FTI関係の傾きの逆数がどれも全て連結橋一個の「エネルギー張力変換比率」を直接的に反映すると仮定すると，種々の干渉によってU-Fp関係，U-PVA関係，U-FTI関係の傾きがどの様に変化するかを観測することは，種々の干渉によって連結橋一個の「エネルギー張力変換比率」がどの様に変化するかを観察していることになる。しかしU-Fp関係，U-PVA関係，U-FTI関係の傾きの逆数全てがそれを直接的に反映しているはずがない。なぜなら前述のように様々な干渉を与えた時，これらの傾きはそれぞれ異なった反応を示しており，一定した傾向にないからである。どの関係の傾きが連結橋一個の「エネルギー張力変換比率」を表す指標として適切か。この疑問はそれらの関係の傾きがf/eAとどの様な関係にあるかが分かった時に明らかになる。

連結橋一個の「エネルギー張力変換比率」は心不全や虚血性心疾患においてはとりわけ重要となる。エネルギー張力変換比率が高ければ同じ消費エネルギーでより大きい張力を発生出来ることになり，不全心や虚血性心疾患にとっては好都合である。このような作用を持つ薬剤がそれらの疾患にとって好ましいであろう。

10.2 Um-Fp関係，Um-PVA関係，Um-FTI関係の傾きとeA/fとの関係

U-Fp関係，U-PVA関係，U-FTI関係の傾きの逆数は連結橋回転に必要なエネルギー(cross-bridge cycling energy: Um)に関する効率であり，細胞の基礎代謝に相当する基礎的消費エネルギー（非機械的エネルギーとも言う）に関しては情報を含んでいない。心筋収縮における全消費エネルギー(U)と機械的パラメーターとの関係（即ち，U-Fp関係，U-PVA関係，U-FTI関係）の傾きの替わりに，連結橋回転エネルギー(Um)と機械的パラメーターとの関係（即ち，Um-Fp関係，Um-PVA関係，Um-FTI関係)の傾きを分析しても同じことである。ここではU-Fp関係，U-PVA関係，UFTI関係の傾きの替わりに，それらと等価であるUm-Fp関係，Um-PVA係，Um-FTI関係の傾きをモデルを用いて数式で表現し，それらがeA/fとどの様な関係にあるかを調べる。

一個の活性連結橋が張力を発生しながら単位時間連続して回転する時に消費するエネルギーをeAとすると，ある時間中(dt)にN個の活性連結橋が回転する時の必要エネルギー量(dUm)は式7-1となる177)。

dUm/dt = (eA/f)(F – Fs) (7-1)

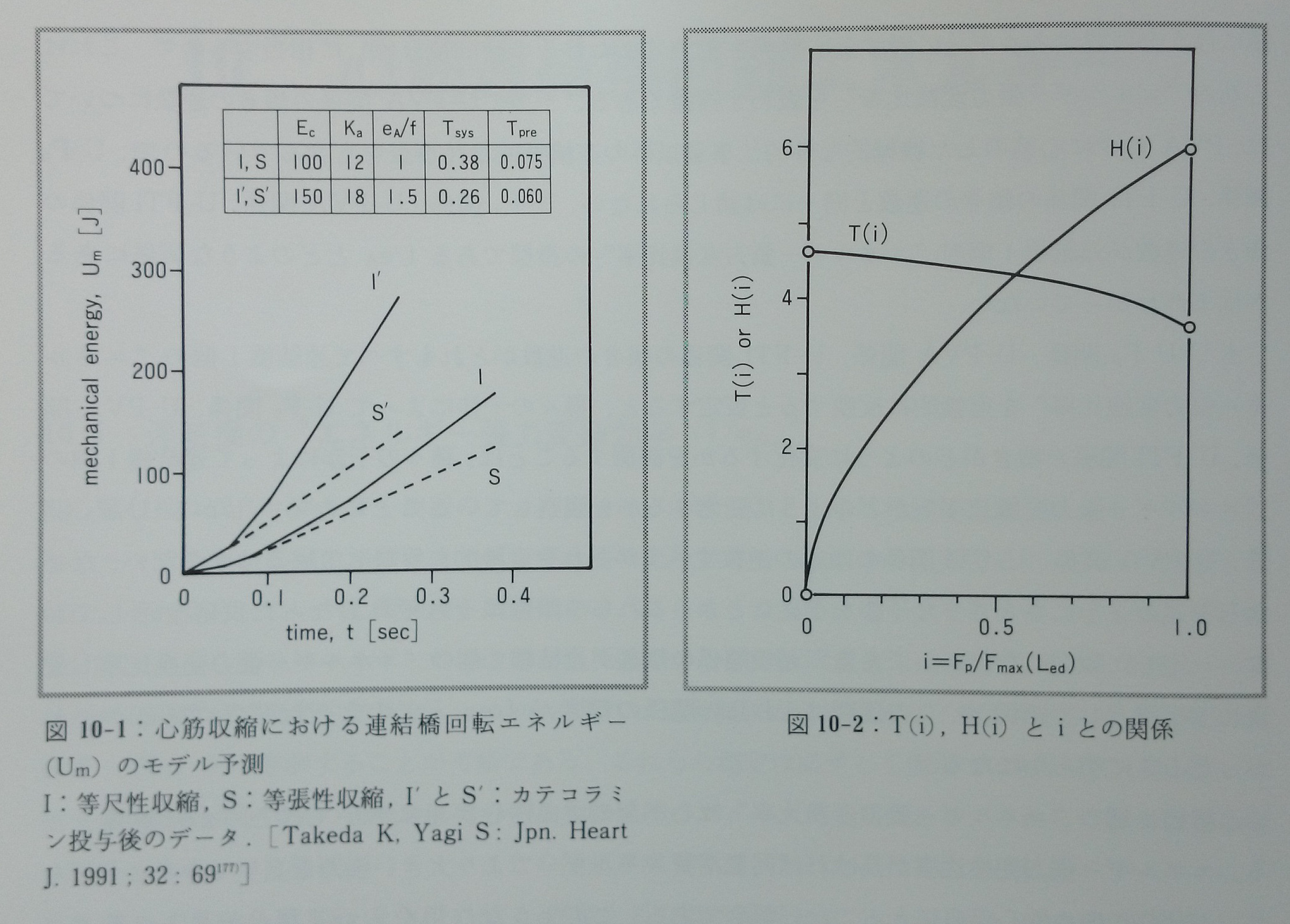
Fsは静止張力であるが，ここではその値は無視した。Umは活性連結橋が回転し張力を発生する際の必要エネルギー量(cross-bridge cycling energy)を表す。Umの値の経時的変化の予測は図10-1に示す。等尺性収縮時(I)のUmは下に凸のカーブとなるが，等張性収縮(S)ではほぼ直線的となる。また同一の初期心筋長からの収縮では，等尺性収縮(I)のUmが等張性収縮(S)のUmより大きな値となる。catecholamine投与(I’，S’)では心筋収縮時間は短縮するが，Umは増大する。

式3-6，3-6’および式7-1から式7-2，7-2’が導かれる177, 178)。式7-2は心筋の一回の等張性収縮による連結橋回転エネルギ－Umと心筋の発生張力Fpとの関係（Um-Fp関係）を表わす。

Um = (eA/f)･Ka-1･T(i)･Fp (7-2)

T(i)= 2 + [(1 – i)/i]･loge(1 – i)-1 (7-2′)
ここに　i=Fp/Fmax(Led)

式7-3は連結橋回転エネルギ－UmとPVAとの関係（Um-PVA関係）を表わす177)。

Um = (eA/f)･(Ec1/2/Ka)･H(i)･PVA1/2 (7-3)

H(i)= {2i/[a(2 – i)]}1/2･T(i) (7-3′)

式7-4は連結橋回転エネルギ－Umと力-長さ面積(force-length-area: FLA) 77)との関係（Um-FLA関係）を表わす177)。FLAはPVAの心筋におけるanalogyである。

Um = (eA/f)･[(aEc)1/2/Ka]･H(i)･FLA1/2 (7-4)

式7-4は式7-3と定数a以外は同一である。即ち，左室のUm-PVA関係と心筋のUm-FLA関係は数学的に等価である。式7-5は連結橋回転エネルギ－UmとFTIとの関係（Um-FTI関係）を表わす177)。

Um = (eA/f)･FTI (7-5)

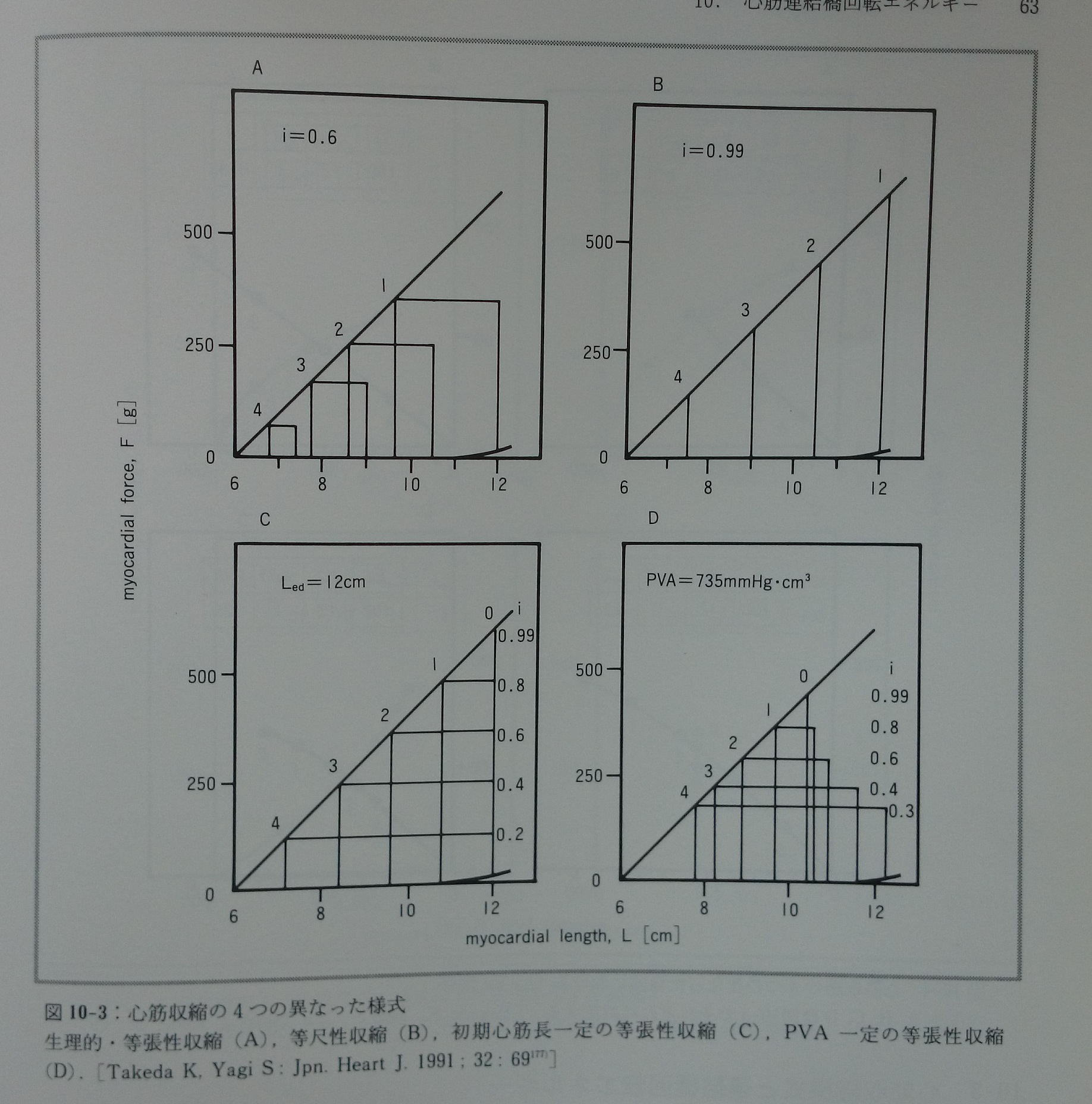
以上から，Um-Fp関係，Um-PVA関係，Um-FTI関係の傾きと連結橋一個の「エネルギー張力変換比率」であるf/eAとの関係が数式で表現された。なお，T(i)，H(i)とiとの関係は図10-2に示す。

Um-Fp関係の傾きは(eA/f)･Ka-1･T(i)，Um-PVA関係の傾きは(eA/f)･(Ec1/2/Ka)･H(i)，Um-FTI関係の傾きは(eA/f)で表現され，どの関係の傾きもf/eAの逆数に比例する。とりわけUm-FTI関係の傾きは(eA/f)そのものであり，この関係の傾きこそが連結橋一個の「エネルギー張力変換比率」の逆数を表す。様々な状態におけるUm-Fp関係，Um-PVA関係，Um-FTI関係の傾きの多様な変化をこの理論式が整合性を持って説明できるかどうかを以下で検証する。

10.3 心筋収縮様式と連結橋回転エネルギー

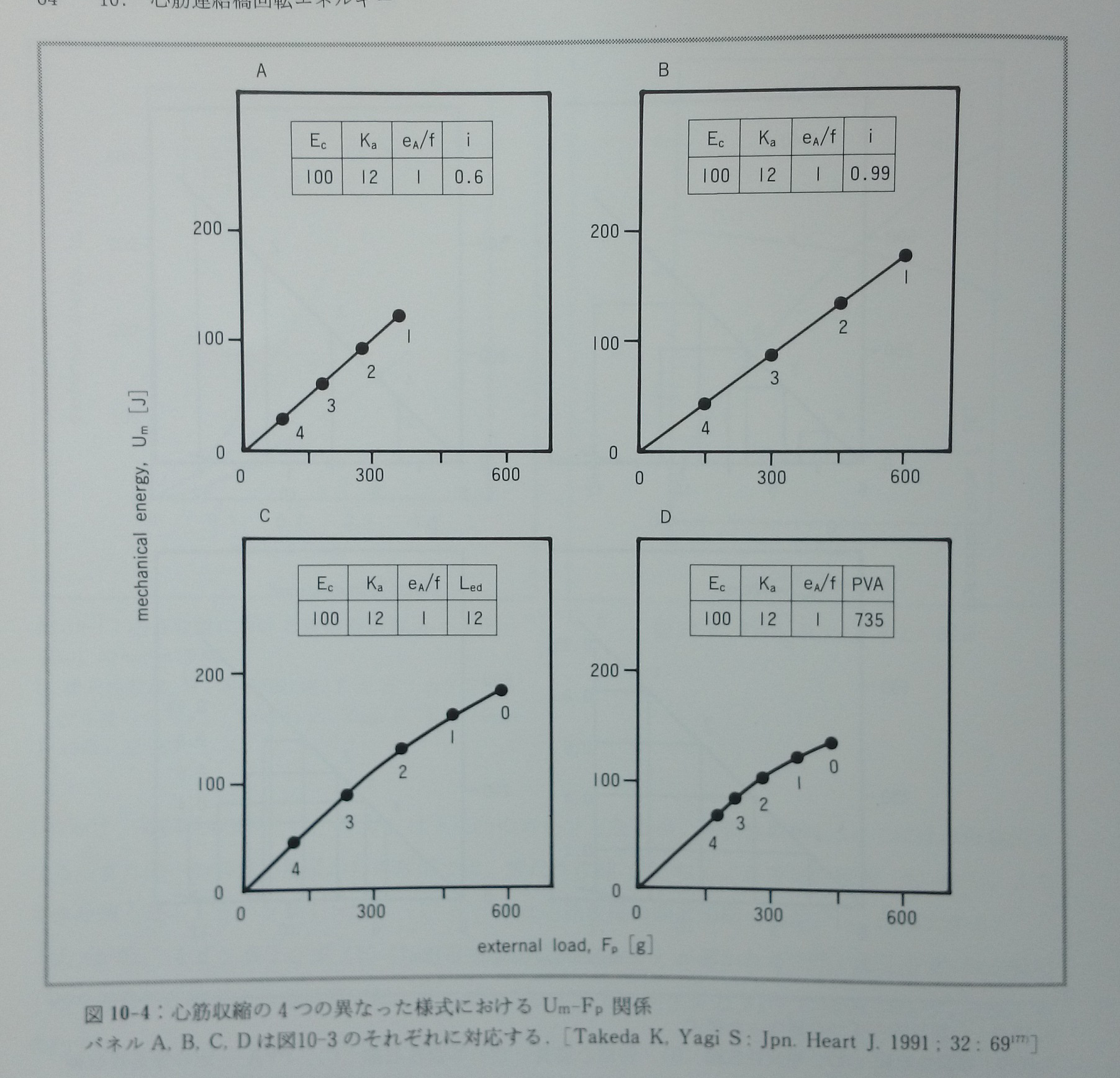
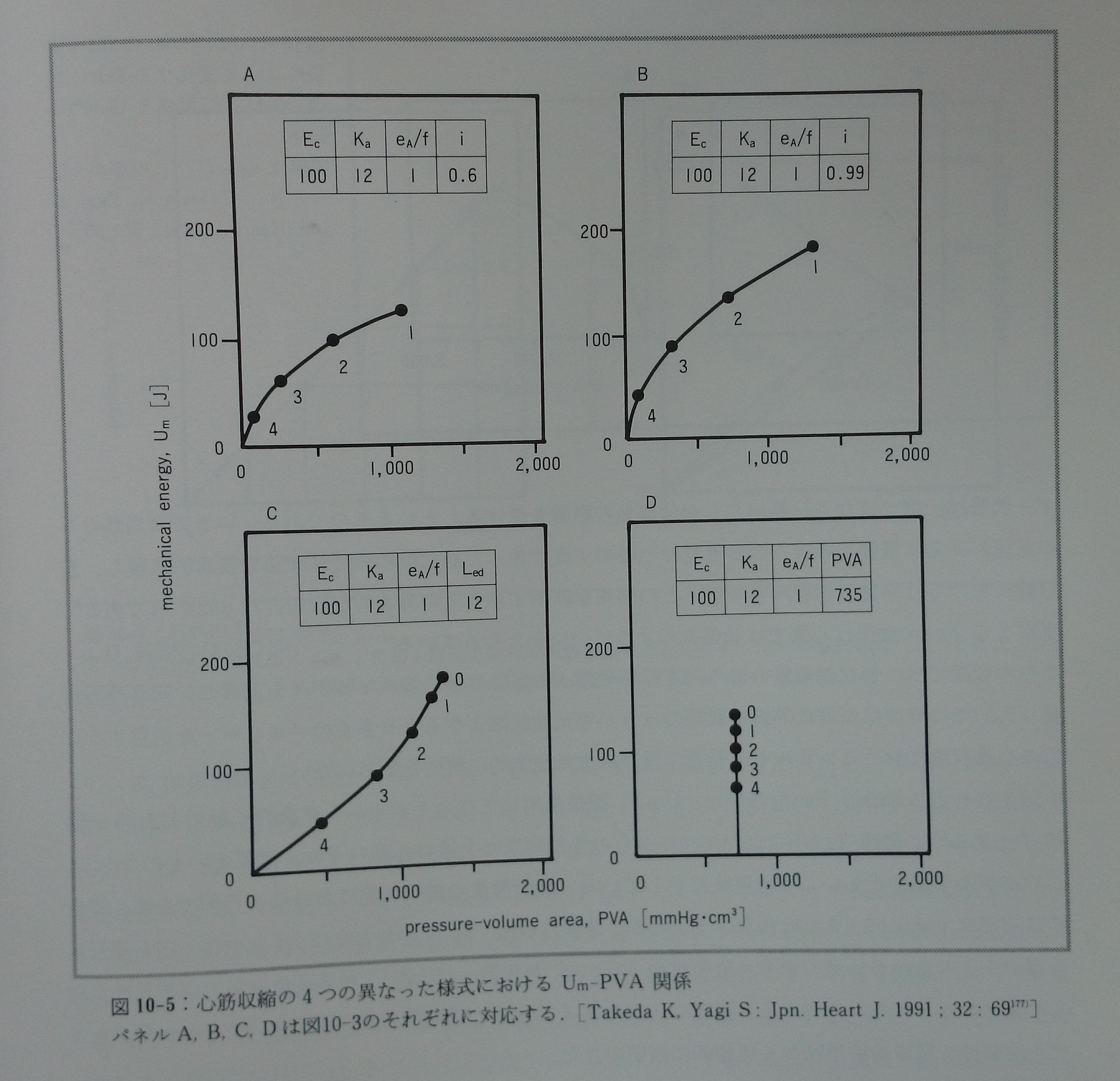
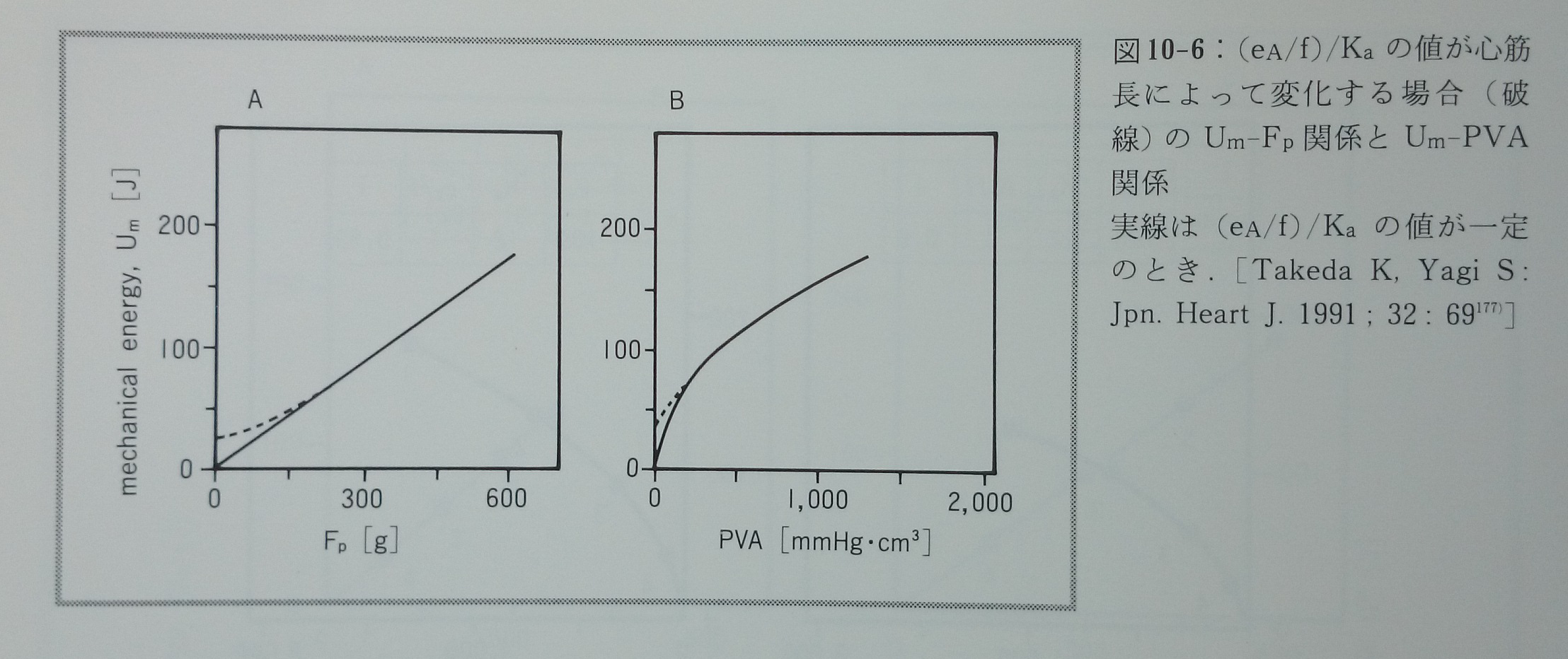
心筋収縮の異なった四つの様式（図10-3）におけるUm-Fp関係（図10-4）とUm-PVA関係（図10-5）を推測する177)。Um-Fp関係は収縮様式にあまり依存しないが，Um-PVA関係は収縮様式によって劇的に変化する。Um-FTI関係は収縮様式と無関係に基本的な直線関係にある。生理的収縮様式ではPVAの値が大きい時，Um-PVA関係は直線関係に近似されるが，PVAが小さい時には明らかに上に凸のカーブとなる。実際に報告されたVO2-FLA関係やVO2-PVA関係の一部に少数ではあるがこの様な特徴を示すものが認められる（文献77)の図3A ，文献154)の図2，文献157)の図2A）。PVA一定の収縮様式ではiの低下に対応してUmも低下し，その他の収縮様式と際立った対比を示す（図10-5）。PVA一定の収縮様式ではiの値に無関係に常にVO2は一定であると菅らは報告している155)。最近PVA一定の収縮様式においてこのモデル予測と同じ結果を竹内ら182)が報告している。このモデルでは(e A/f)/Kaの値は常に一定であることを前提とした。もしこの値が心筋長によって変化し，特に心筋長が短い時にはこの値が大きくて心筋長が増大するにつれて低下するのであれば，モデルから予測されるUm-PVA関係はもっと直線に近いものとなる。またUm-Fp関係は心筋長の短い範囲で緩やかなカーブとなる177)（図10-6）。図10-6で示した関係がこれまでに報告された実測値に近い。Kaは心筋長に依存することが分かっている169, 170)。(eA/f)/Kaの値は心筋長に依存して変化する性質を持つかも知れない。

10.4 心筋のFenn効果

カエル縫工筋での実験から得られ，1923年に発表されたFenn効果45)とは「筋収縮に伴うエネルギー消費は一定ではなく，筋肉のした仕事量の影響を受ける」と言うものである。今では当然のこの記述が非常に重要なのは，この発見は当時の主流であった筋収縮の弾性体理論を根本的に覆し，筋収縮における仕事量と消費エネルギーとの関係を理解する上の基本的な原理となったからである91)。現在このFenn効果は心筋では通常次のように言い換えられている28, 138, 140)。「同じ初期心筋長(Led)からの収縮では，等尺性収縮の方が等張性収縮よりもより多くのエネルギーを消費し，同じ外的負荷(Fp)では今度は反対に等張性収縮の方が等尺性収縮よりもより多くのエネルギーを消費する」。この心筋収縮におけるエネルギー消費の違いは未だ理論的に解明されていない。

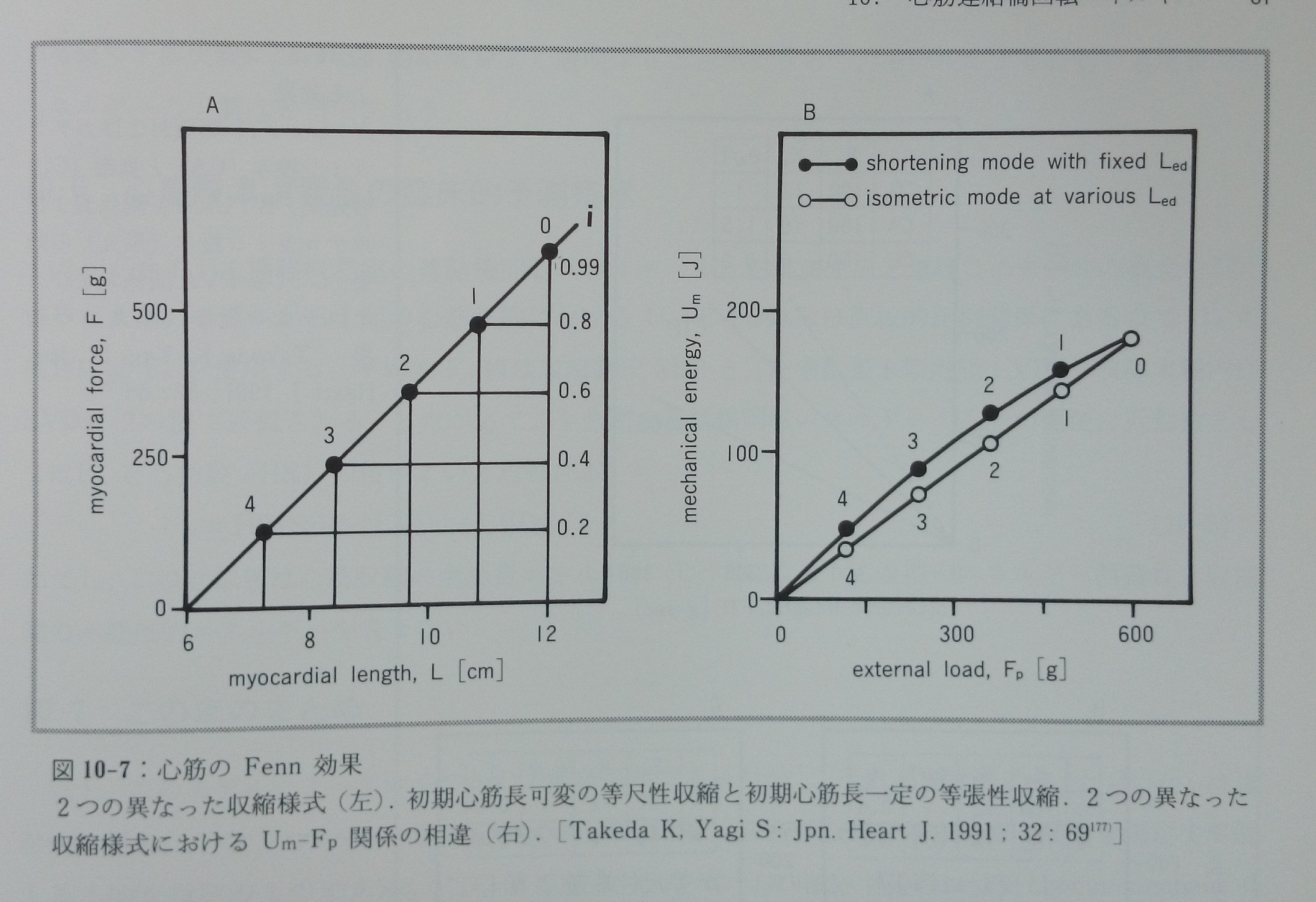
以上の心筋におけるFenn効果を，Um-Fp関係を用いてこのモデルから理論的に説明したのが図10-7である177)。図10-7に示されたモデルからの予測結果は上述の心筋のFenn効果そのものであり，このモデル予測が正しいことを明快に示している。問題解決の鍵は収縮におけるiの値である。等尺性収縮ではiは0.99(または0.95)であるが，等張性収縮ではiが例えば0.5と少なくとも等尺性収縮のiよりも小さい値であり，そのためT(i)（式7-2，式7-2’）が等張性収縮では等尺性収縮より大きな値となるからである（図10-2）。長い間その現象の理論的背景が謎であったFenn効果をモデルは初めて現象論的ではなく理論的に解決した。

10.5 catecholamine，低温，甲状腺機能低下

様々な干渉を与えた時のVO2-PVA関係の傾きの変化が調べられた結果，catecholamine，α遮断薬，Ca2+，Ca2+拮抗剤，ジギタリス，ミルリノン，サルマゾール，低体温等でVO2-PVA関係の傾きは有意に変化しなかった163)。このように異なった種類の多くの干渉を与えても変化しないVO2-PVA関係の傾きのことを菅らはVO2-PVA関係のstoichiometryと呼んだが，その現象の理由は分かっていない。catechlomine投与9, 59, 157)や低体温9, 111, 153)はU-Fp関係とU-PVA関係においてその傾きを変えない。U-FTI関係の傾きはU-PVA関係やU-Fp関係と全く対照的に，同じ干渉を与えると容易にその傾きが変化する。甲状腺機能異常ではU-FTI関係81)，U-Fp関係81, 112)，U-PVA関係63)全ての傾きは変化する。ただしU-PVA関係で変化しないとする報告もある161)。

Um-Fp関係の傾きは(eA/f)･Ka-1･T(i)，Um-PVA関係の傾きは(eA/f)･(Ec1/2/Ka)･H(i)，Um-FTI関係の傾きは(eA/f)で表される（式7-2，7-3，7-4）。これらの傾きは全て(eA/f)，Ec，KaとT(i)またはH(i)の５つのパラメータの組み合わせである。このパラメータの大雑把な意味はEcは細胞内[Ca2+]に関連し，KaはCa2+とトロポニンCとの反応速度定数でありその値は心筋収縮時間の逆数に比例する，(eA/f)はmyosin ATPaseのchemo-mechanical transduction活性に比例する。iは心筋の前負荷，後負荷，心筋収縮性の三つの相互関係によって決定される因子であり（図7-8），その値はEcの変化と反対方向へ変化する。T(i)はEcの変化と同じ方向に小さく変化し，H(i)はEcの変化と反対方向へ大きく変化する。心筋に与えた干渉が以上の５つの因子にそれぞれどの様な変化を起こすかが予め分かればUm-Fp関係，Um-PVA関係，Um-FTI関係の傾きがそれぞれどの様に変化するかが理論的に推測できるはずである。

catecholamineはEcとKaを共に増加させるが110, 149, 159, 160)，心筋冷却はEcを増大させ58, 102, 111, 122, 153)，Kaを低下させる102, 153)。また甲状腺機能低下ではEcとKaは共に低下する81)ことがこのモデルから推測されている。心筋の化学的エネルギーから機械的張力への変換はmyosin ATPaseによってなされる。myosin ATPaseのこのchemo-mechanical transduction活性(eA/f)はcatecholamineで増大するが211)，心筋冷却3)や甲状腺機能低下3, 81)では低下する。心筋収縮における前述のU-Fp関係，U-PVA関係，U-FTI関係の傾きが種々の干渉で複雑に変化するのは，このeA/f，Ec，Ka，T(i)，H(i)などの種々の干渉に対する反応の違いによってもたらされている。

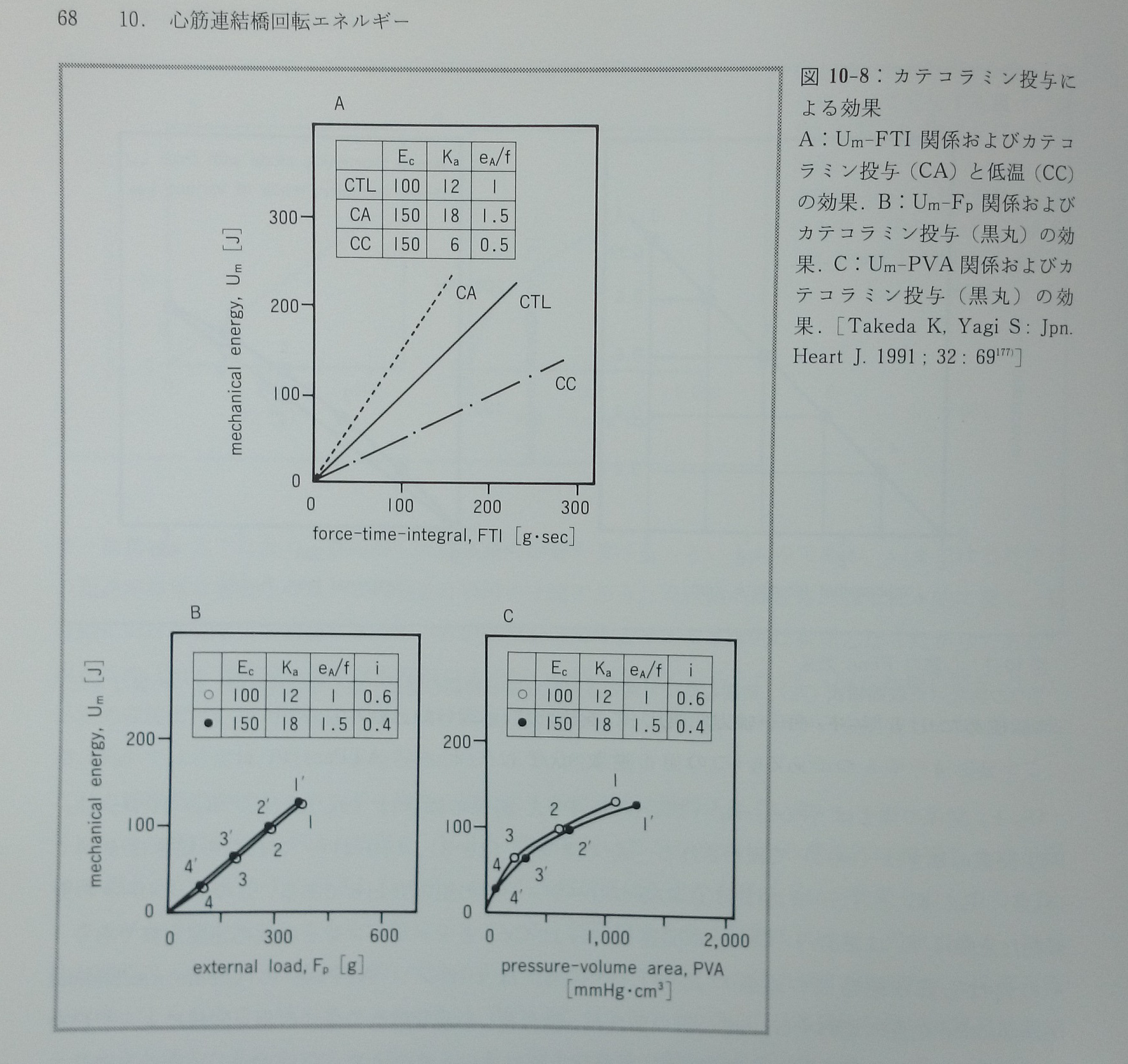
catecholamineはEc，Ka，eA/fのすべてを増大させる。もしcatecholamineによってEc，Ka，eA/fがすべて50%増加すると仮定すれば，Um-Fp関係，Um-PVA関係，Um-FTI関係の傾きはそれぞれ+4%，-3%，+50%変化すると数式から計算された177)。この結果はcatecholamineによってUm-Fp関係とUm-PVA関係の傾きは変化せず，Um-FTI関係の傾きは大きく増大することを意味する（図10-8）。低体温によってEcは増大し，KaとeA/fは低下する。低体温によってEcは50%増大し，KaとeA/fは50%低下すると仮定するとUm-Fp関係，Um-PVA関係，Um-FTI関係の傾きはそれぞれ+4%，-3%，-50%変化すると計算された。この結果は低体温によってUm-Fp関係とUm-PVA関係の傾きは変化せず，Um-FTI関係の傾きは大きく低下することを意味する（図10-8）。甲状腺機能低下によってEcは24%低下し，Kaは30%低下し，eA/fは44%低下するので81)，Um-Fp関係，Um-PVA関係，Um-FTI関係の傾きはそれぞれ-20%，-25%，-44%変化するとモデルから計算された。実測値はそれぞれ-26%81)，低下するが値は不明63)，-40%81)変化した。以上のようにモデルはcatecholamine，低温，甲状腺機能低下と言う心筋収縮性に全く異なった影響を与える代表的三種類の干渉実験における実測結果をよく説明することが出来る177)。モデルによる心筋の連結橋回転エネルギーの予測は妥当であろう。

10.6 心筋酸素消費量の臨床的予測指標

ベッドサイドで簡略に左室の連結橋回転エネルギ－Umを推測する時はこのモデルの概念を利用すると良い。モデルから一回の心筋収縮におけるUmとFpはほぼ直線的比例関係にあるのでUmの推定にはFpを使用する。平均的Fp値は収縮期圧SBPと（左室拡張末期内径LVDd＋収縮末期内径LVDs）/２の積で近似される。従って，一分間の連結橋回転エネルギ－(Um)の簡便な近似法としてはFpと心拍数(HR)の積が良いと思われる。

Um ∝ HR･SBP･(LVDd + LVDs)/2 (7-6)

ただし，この近似値は心筋収縮の全消費エネルギ－(U)ではなく，拡張期のエネルギー消費量と収縮期の非機械的エネルギーを含まない。

10.7 この章のまとめ

以上，このモデルによって幾つかの予測が可能であったが177)，それらをまとめると，

１）f/eAは連結橋一個あたりの「エネルギー張力変換比率」を表す。これは心臓のエネルギー効率を決定する最も基本的な指標の一つである。この値の逆数eA/fはmyosin ATPaseのchemo-mechanical transduction活性に関係する。
２）(eA/f)/Kaは心筋長に依存して変化する。
３）Um-FTI関係はこのeA/fを比例定数とした直線である。
４）Um-Fp関係はほぼ直線でありその線形性は収縮様式とほぼ無関係である。関係の傾きは(eA/f)･Ka-1･T(i)である。
５）Um-PVA関係は大きな値のPVA領域では近似的に直線であるが，小さな値のPVA領域では上に凸のカーブである。関係の傾きは(eA/f)･(Ec1/2/Ka)･H(i)である。PVA一定の収縮様式では特異なUm-PVA関係を示す。
６）Um-Fp関係とUm-PVA関係の傾きはEcの変化には比較的影響されにくいが，eA/fとKaの変化には影響を受けやすい。
７）Um-FLA関係はUm-PVA関係と等価である。

モデルによる連結橋回転エネルギ－(Um)予測と過去の実験事実との対比から，このモデルは実際に観察された様々な心筋・心臓収縮のエネルギ－的特性を理論的によく説明できた。とりわけ長年その現象の原因が解明されなかった心筋のFenn効果や，catecholamine，低温，甲状腺機能低下による心筋収縮性変化に際するU-Fp関係，VO2-PVA関係，U-FTI関係の異なった反応に対してモデルは理論的に良く説明し，このモデルの妥当性を理論的に立証した。

前述した様に極めて単純な仮説にもとずくこのモデルが高度に複雑な心筋収縮の三つのレベルの基本的力学特性とエネルギー特性を整合性よく説明できた理由の一つは，心筋収縮に関係する数多くの因子のなかで，筋小胞体から放出される[Ca2+]の値と[Ca2+]がトロポニンCと結合する化学反応が最も重要な決定因子であるためであろう。