心臓の活性化理論と心不全■ ３.円筒モデル

2014年1月1日竹田幸一心臓の活性化理論と心不全

■ ３.円筒モデル

3.1 円筒モデルの構築

生理的左室壁心筋においてEcを計測するための数学モデルを設定するにあたり，実際の左室壁心筋の力学的構造を大胆に単純化した。単純化によるモデルとしての正確性の低下は避け難い。しかし，モデルや理論はその原理が単純である方が複雑な自然現象の整理と理解を容易にするという大きな利点を持つ。更に完壁なモデルや理論というものは本来存在し得ない。それは自然現象への適合の度合いによって，その妥当性が相対的に評価されるものでしかない。従って，生理的左室壁心筋のEcを直接測定できる実際的な方法が未だない現状では，それらを近似できる方法としてこのモデルは意味がある。

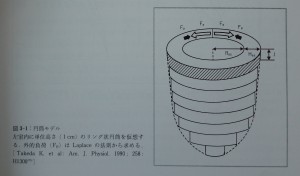
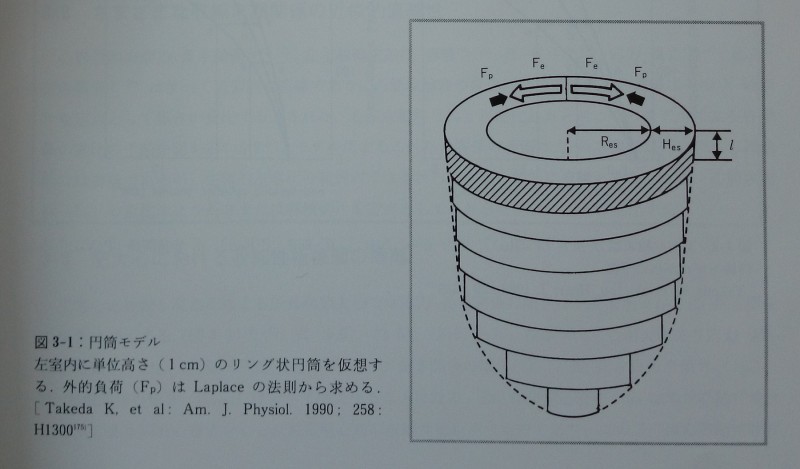
モデルにおける仮説を定義する174)。1）左室内に単位高さ(1cm)のリング状円筒を仮想する（図3-1）。円筒を形成する左室壁心筋において円周方向の収縮末期の力(Fes)と心筋長(Les)は直線的比例関係にあり，その比例定数をEcとする(式2-1)。2）左室壁に加わる外的負荷（Fp)はLaplaceの法則から求める。3）収縮末期とは左室壁心筋に発生する収縮力と左室壁の収縮を妨げる外的負荷とが均衡した点である(Fes=Fp)。以上の仮説から左室収縮末期力－長さ(式2-1)，応力－歪み(式2-2)，圧－長さ(式2-3)，圧－容積関係(式2-4)を表す数式が得られる174)（図3-2）。

Fes = Ec(Les – Lo) (2-1)

Ses = 2πEc･t/[[Mo/πRo2+(1+t)2]1/2-(1+t)] (2-2)

Pes = 2πaEc(1 – Lo/Les) (2-3)

Pes = 2πaEc[1 – (Vo/Ves)1/2] (2-4)

Fes＝収縮末期収縮力 [g], Ec＝収縮末期心筋弾性 [g/cm], Les＝収縮末期心筋長 [cm],Lo＝基準心筋長 [cm], Res＝収縮末期円筒半径 [cm], Ro＝基準円筒半径, Ses＝収縮末期応力 [g/cm2], t＝収縮末期心筋歪み=(Les-Lo)/Lo=ΔL/Lo, Mo＝円筒心筋体積＝π[(Res+Hes)2-Res2] [cm3], Hes＝収縮末期円筒壁厚 [cm], a＝変換定数＝0.735mmHg/g/cm2, Pes＝左室収縮末期圧 [mmHg], Ves= 収縮末期円筒容積 [cm3],Vo= πRo2＝基準円筒容積 [cm3].

左室圧がゼロの時の左室収縮末期応力－歪み関係の傾きEto，圧－内径関係の傾きEso，圧－容積関係の傾きEmaxoとEcの理論的関係はそれぞれ式2-5，2-6，2-7である174)。ただしHoは左室圧がゼロの時の左室壁厚である。

Eto･Ho/Ro = 2πEc (2-5)

Eso･Ro = πaEc (2-6)

Emaxo･Vo = πaEc (2-7)

導かれた簡単な数式は左室収縮末期関係に関する幾つかの知見を理論的に説明することができる174, 181)。

3.2 様々な収縮末期関係の近似的直線性

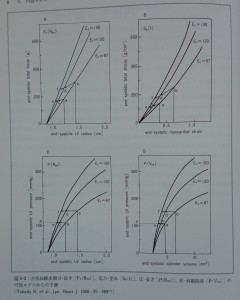
心筋収縮末期力－長さ関係32, 87, 150)，左室収縮末期圧－容積159, 160)，圧－長さ110, 114)，応力－長さ115, 187)，応力－歪み関係121, 205)はすべて近似的に直線であり，心筋収縮性の変化によってこれらの直線はそのx軸切片を定点として傾きが変化するとされる。心筋収縮性(Ec)が変化した時，このモデルによる各関係の変化の予測を図3-2に示す174)。モデルによるこれらの関係の予測は力－長さ関係以外いずれも理論的には曲線であるが，生理的左室圧の範囲内ではそれらはみな近似的に直線と見なし得る。心筋収縮性(Ec)の変化により長さ又は容積切片を定点としてそれらの関係の傾きは変化する。

3.3 肥大心における収縮性指標間の乖離

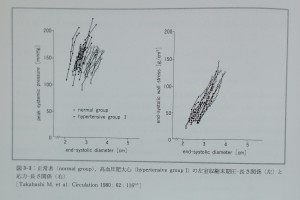
正常心と比較し高血圧による肥大心では応力－長さ関係の傾きは不変であるが，圧－長さ関係の傾きは増大する（図3-3）146, 167)。式2-5，2-6，2-7から，壁厚(Ho)の増大により応力－歪み関係の傾き(Eto)とRoが一定であっても，力－長さ関係の傾き(Ec)，圧－長さ関係の傾き(Eso)，圧－容積関係の傾き(Emaxo)はすべて増大することになる。Etoは単位心筋の，Ecは単位心筋の集合である或る固有の厚さをもった左室壁心筋の収縮性能を示すものであり，この２つは心収縮性評価の対象が異なる。従って，上述のようにEtoとEcとの間に増減の乖離が生じる。Etoは心筋収縮性の絶対的評価に，Ecは固有の壁厚をもつ個人の左室壁性能の評価に適する。

3.4 円筒モデルの限界

円筒モデルには幾つかの明らかな限界がある。１）左室壁心筋の発生張力を得るために左室を薄壁円筒に近似したことである。左室は厚い心筋からなっているので厚さを無視したこのモデルは明らかに欠陥モデルである。将来は心筋の発生張力を得るために現実の左室に近いモデルである厚壁回転楕円体などを考慮すべきである。また左室壁の子午線方向張力は全く無視している。２）心筋の発生張力を得るためにどのような力学モデルを設定しようとも，それは計算による発生張力の推測値であって実測値ではない。将来は左室心筋の発生張力を実測できれば理想的である。３）モデルを簡略化するため，心筋の拡張期静止張力(resting tension)を無視した。正常心筋ではそれほどの問題とならないであろうが，肥大心筋や不全心筋ではこの拡張期静止張力が無視し得ないほど大きくなり，これを無視した予測は実測値から大きくはずれてしまう。将来はこの静止張力を考慮しなければならない。４）収縮末期の定義はこのモデルでは心筋の発生張力と圧による壁応力が均衡した時点とした。現実にはこれに加えて短縮運動による心筋の加速度や心筋の内部抵抗等も考慮しなければ正確な収縮末期点を決定できない。正確な収縮末期点の確定も将来の重要な課題である。