■ 7.心筋収縮時間
7.1 Systolic Time Intervals
Systolic time intervals (STI)は百年以上前から研究され17, 54, 113, 210),臨床において心機能の指標として経験的に利用されてきた古い歴史を持つが,その心臓生理学的意義は長い間明らかではなかった。STIにおける主要な三つのパラメーターとはQ-II時間(QS2時間),前駆出時間(PEP),左室駆出時間(LVET)である。QS2時間は前負荷や後負荷に比較的影響されないが108),PEPとLVETは様々な心疾患において互いに反対方向にその値が変化する206)。QS2時間はβ遮断薬によって延長し15),心筋収縮性を増大させる薬剤によって短縮する21, 49, 208)。QS2時間はSTIの中では心筋の陽性変力作用の判定に最も有用である49, 108)。急性心筋梗塞においてはQS2時間はその病態の重症度に反比例して短縮し199),LDHの値199)や尿中カテコラミンの値106)に密に相関する。急性心筋梗塞急性期のQS2時間の異常低値から正常値への回復は臨床状態の回復やLDH値の回復に伴う199)。狭心症発作時にもQS2時間は短縮する20, 107)。QS2時間を心拍数で補正した値は通常ほぼ一定値を示すが,いったん心臓交感神経活動が変動した時はこの活動度を反映して敏感に変化するものと予測される。しかし,この推測の根拠となる心筋の分子生物学的背景は全く不明である。
7.2 モデルによるSystolic Time Intervals
左室心筋収縮時間を表わす方程式がモデルから次のように導かれる170)。Tsys, Tpre, Tejはそれぞれ心筋の全収縮時間,等尺性収縮時間,等張性駆出時間である。iは後負荷(Fp)を拡張末期心筋長における最大心筋発生張[Fmax(Led)]で除した値である。即ち,i=Fp/Fmax(Led)。
Tsys =Ka-1・loge(1 – α)-1 = 3/Ka (7-1)
Tpre = Ka-1・loge(1 – i)-1 (7-2)
Tej = Ka-1・[3 + loge(1 – i)] (7-3)
式7-2と式7-3から式7-4を導く。
Tpre/Tej = loge(1 – i)-1 /[3 + loge(1 – i)] (7-4)
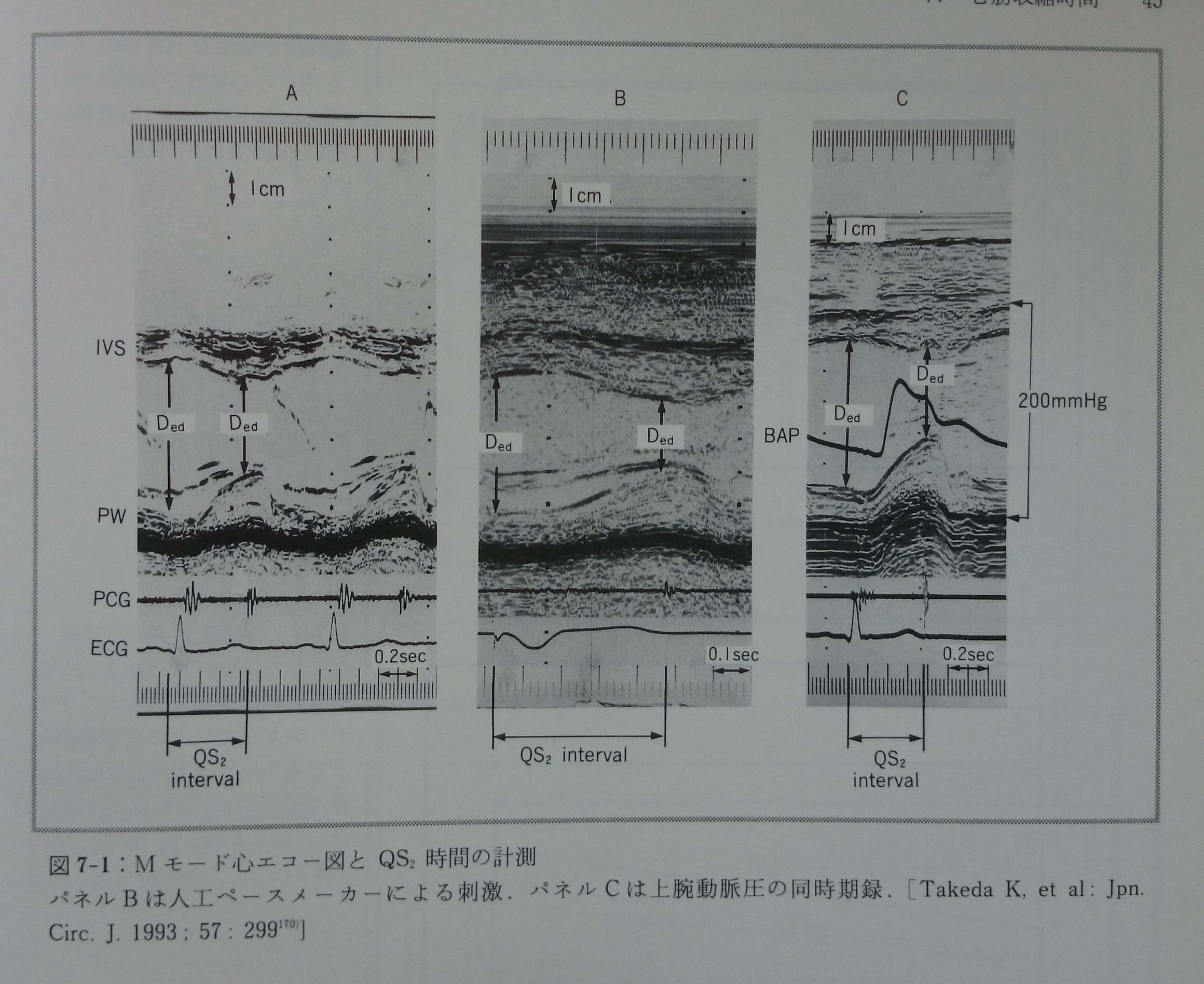
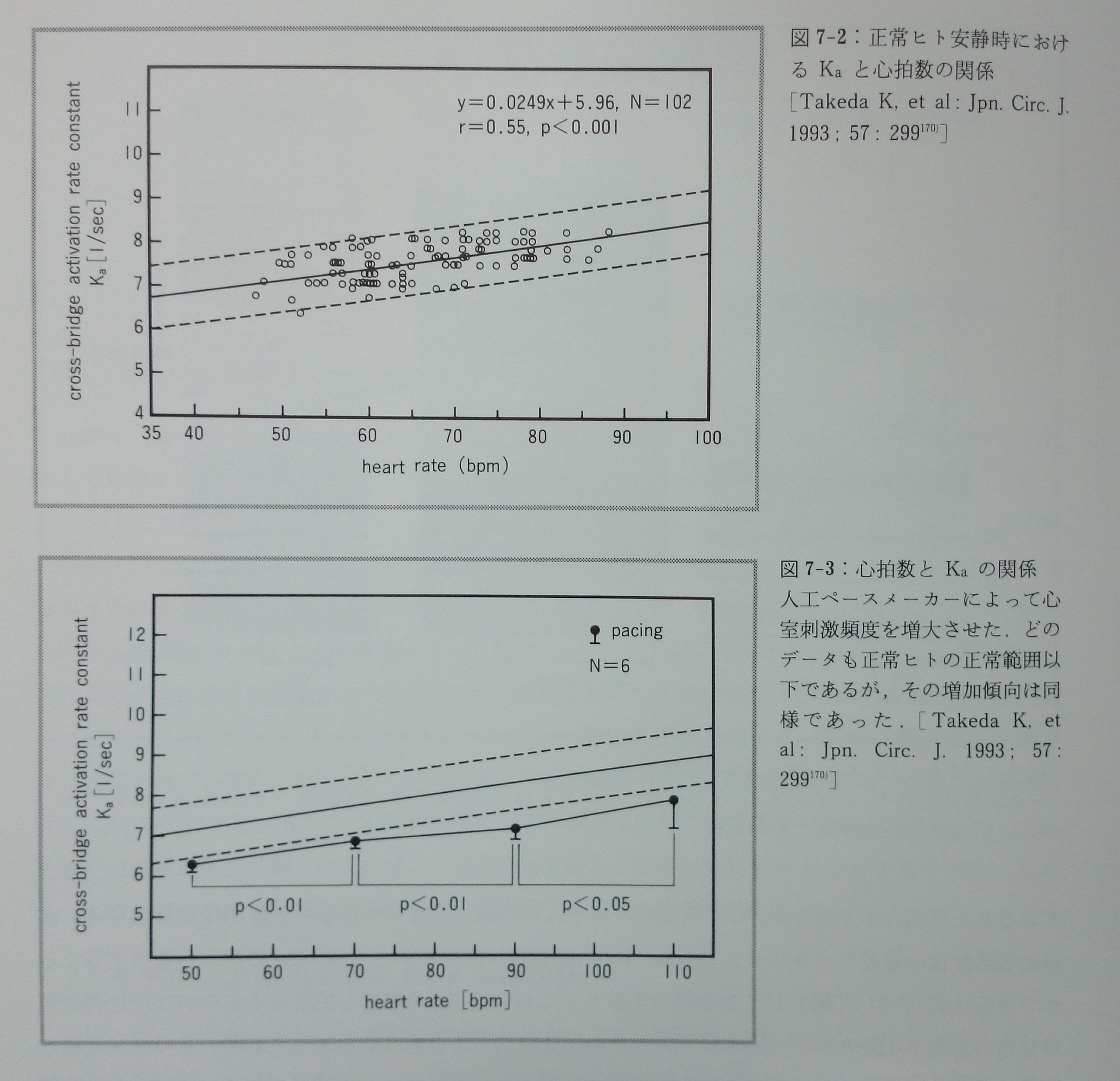
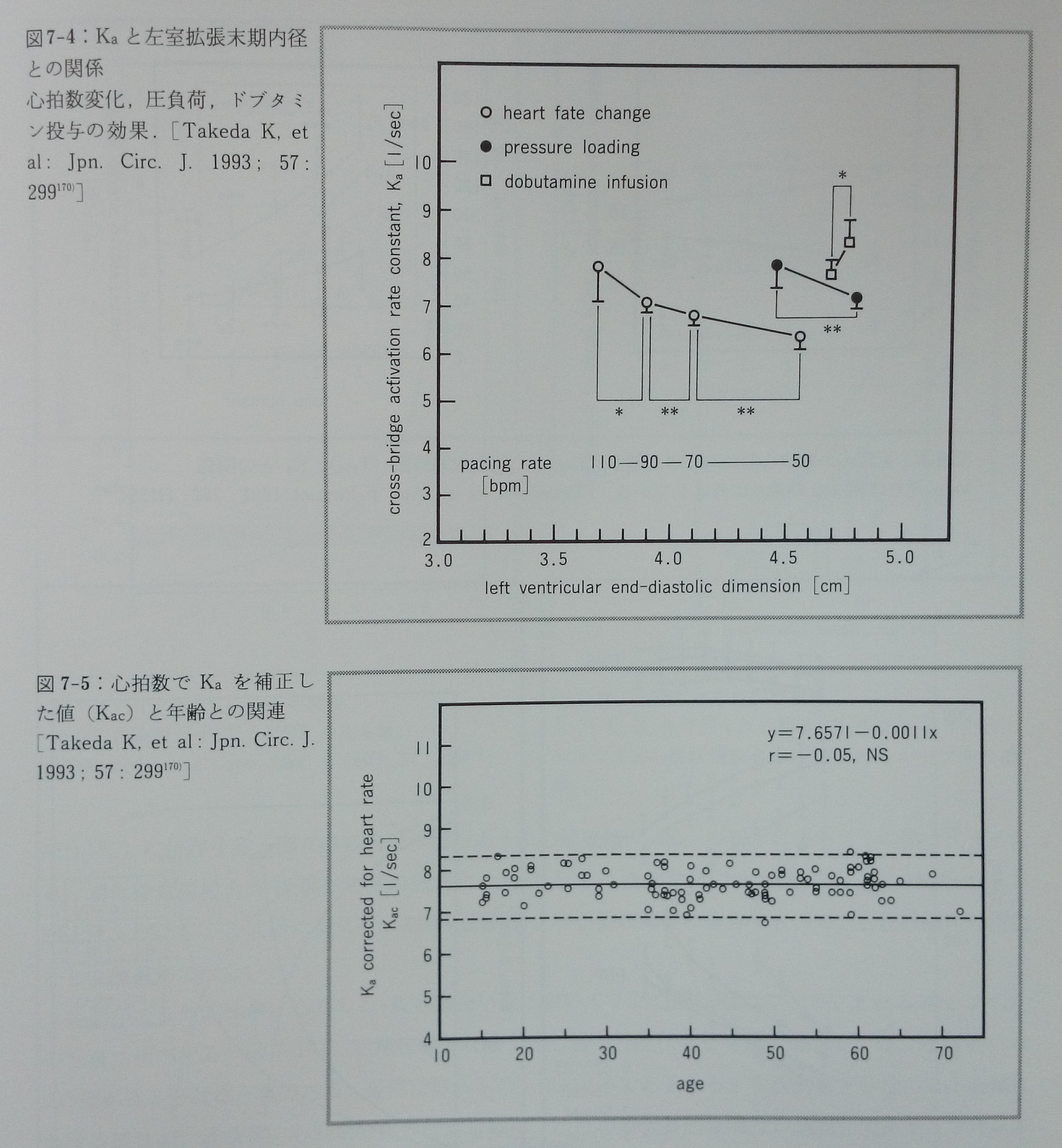
心筋の全収縮時間(Tsys)の値はKaとαのみで,またTpre/Tejの値はiのみで決定される。Tsys, Tpre, Tejをそれぞれ臨床におけるQS2時間,前駆出時間(PEP),左室駆出時間(LVET)に対応させると,モデルからQS2時間は重要な意味を持つことが理解される。式7-1ないし式7-4から,PEP,LVET,PEP/LVETはどれも左室の前負荷および後負荷(正確にはiの値)に影響されることが明らかであるが,QS2時間だけはそれから独立しており,この逆数(Kaに相当する)は連結橋活性化の重要なパラメ-タ-である。Kaの近似値は臨床においてはQS2時間から算出することが出来る(式7-5)(図7-1)。安静時の正常ヒトにおいてKaの値は心拍数とゆるやかな正比例関係の分布にある170)(図7-2)。ペースメーカーで心拍数を増大するとKaも増加するが,その増加曲線は正常ヒトのKaの分布の回帰直線とほぼ平行である(図7-3)。このペースメーカーでのKaを心筋長を横軸に取ってプロットすると,その傾向は圧負荷による心筋の伸長によって表れるKaの変化とほとんど同じであった(図7-4)。従って,安静時の正常ヒトにおいてKaが心拍数と比例関係にあるのは,心拍数によって心筋長が変化し,この変化した心筋長によってKaの値が影響を受けているためであると結論できる170)。心筋長の替わりに心拍数でKaを補正した値(Kac)は年令,性別,心筋長にかかわらずほぼ一定値である170)(図7-5)。KaとKacを求める式は,
Ka = 3/QS2 (7-5)
Kac = Ka + 0.0249(66 – heart rate) (7-6)
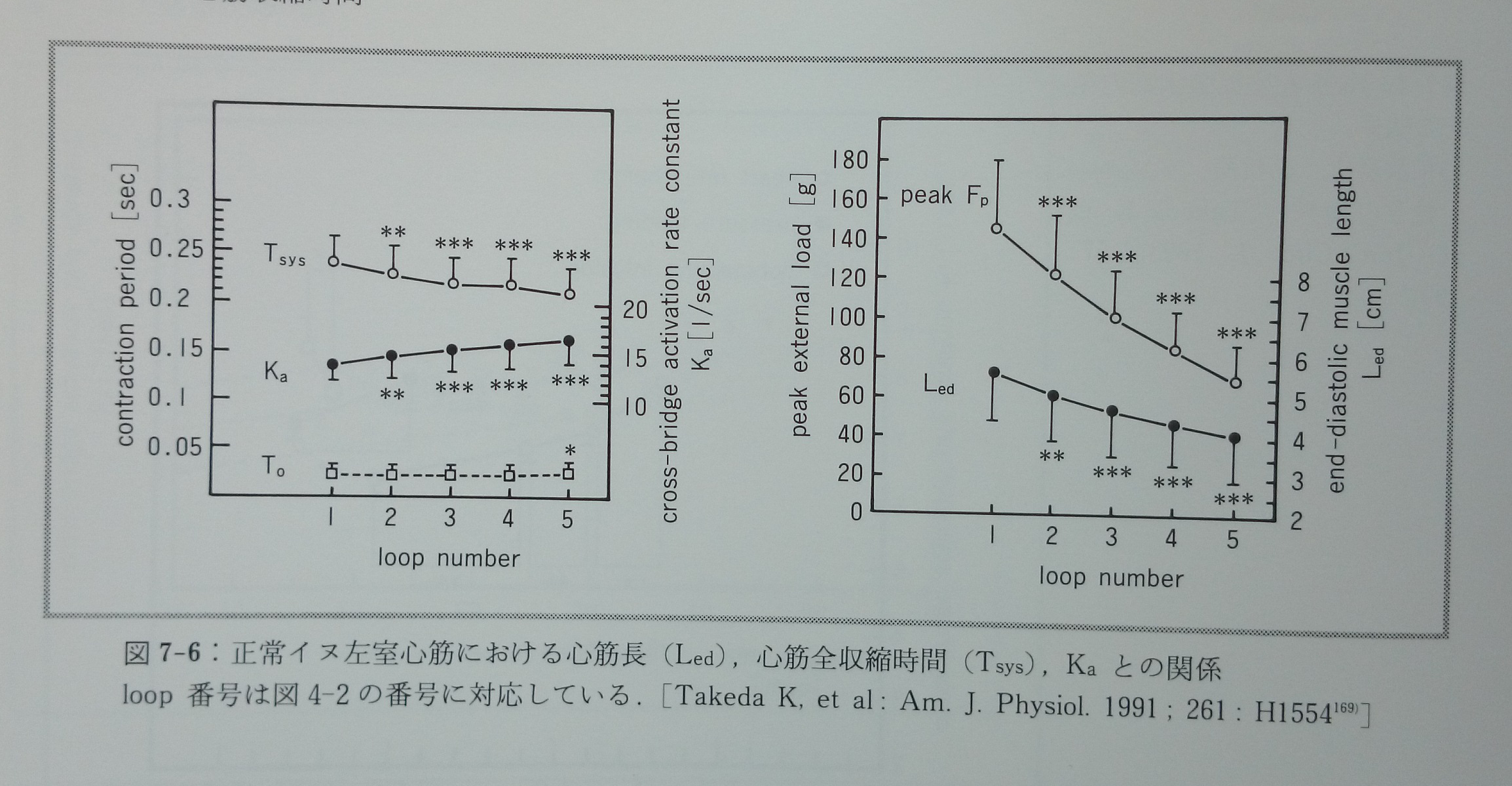
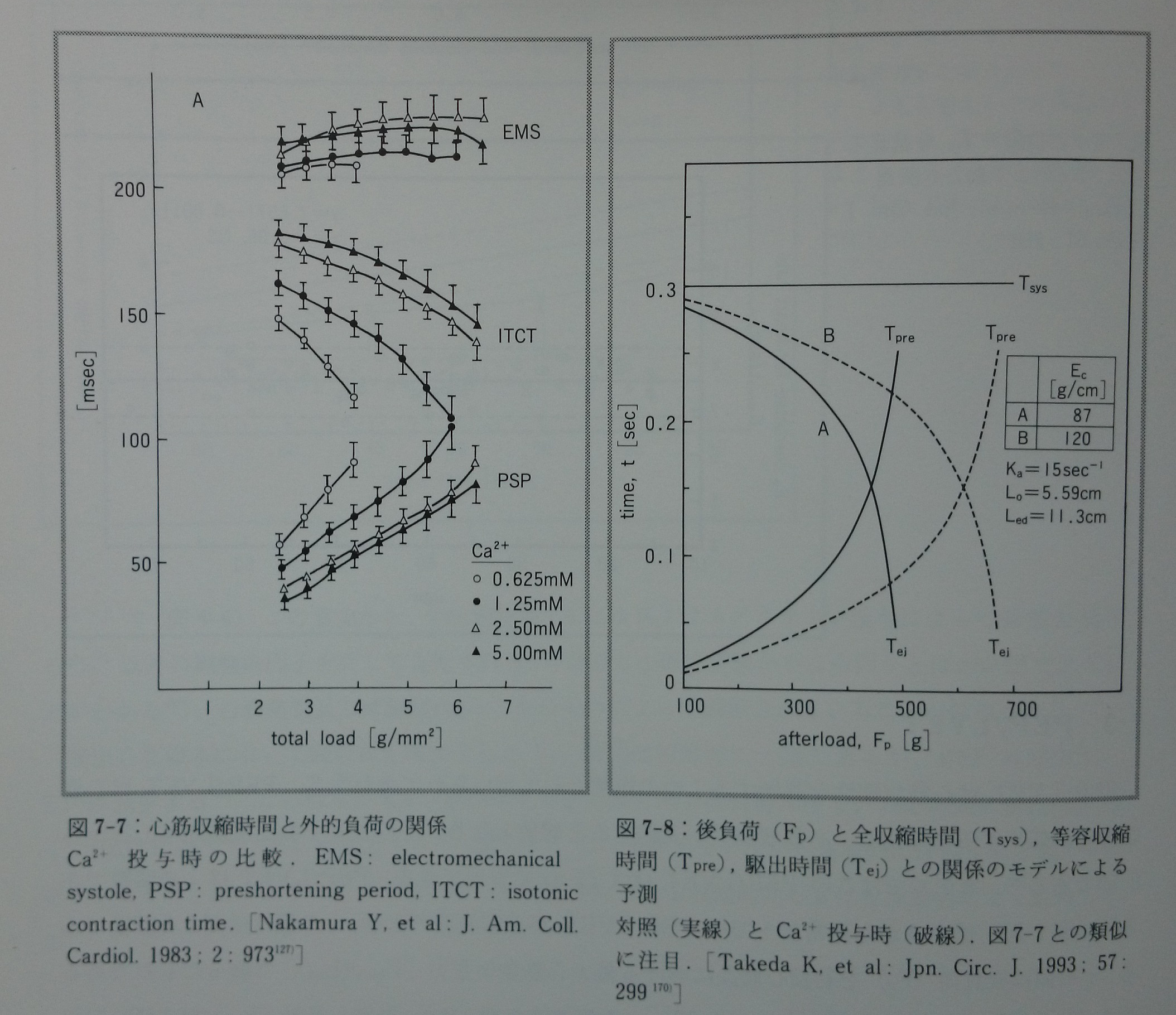
正常イヌ左室心筋においても心筋長を短縮すると心筋の全収縮時間(Tsys)は短くなる169)(図7-6)。心筋標本149)や摘出心臓標本160)において,catecholamineを投与すると心筋発生張力は増大し全収縮時間は短縮する。カルシウムを投与すると心筋発生張力は増大するが,全収縮時間はほとんど変化しない13, 123, 149)(図4-6)。この事実から,全収縮時間(またはKa)はcatecholamine投与によって修飾を受けるCa2+以外の細胞内因子を介して支配されるが(栗原と小西の実験からこの因子とはcAMPであることがわかる99)),心筋発生張力は細胞内Ca2+そのものによって調節されていることが推測される。
摘出心筋標本において後負荷を増加するとTsys時間は相対的に一定であるが,PEPは増大し,ETは減少する127)。この標本にCa2+を投与すると対照と同じ後負荷条件で,Tsys時間に変化は少なく,PEPは減少し,ETは増大する127)(図7-7)。この関係をモデルから理論的に予測すると図7-8の結果となる168)。図の様にモデルは実際の心筋標本における収縮時間の変化を理論的に良く説明できる。
7.3 PEP/LVET
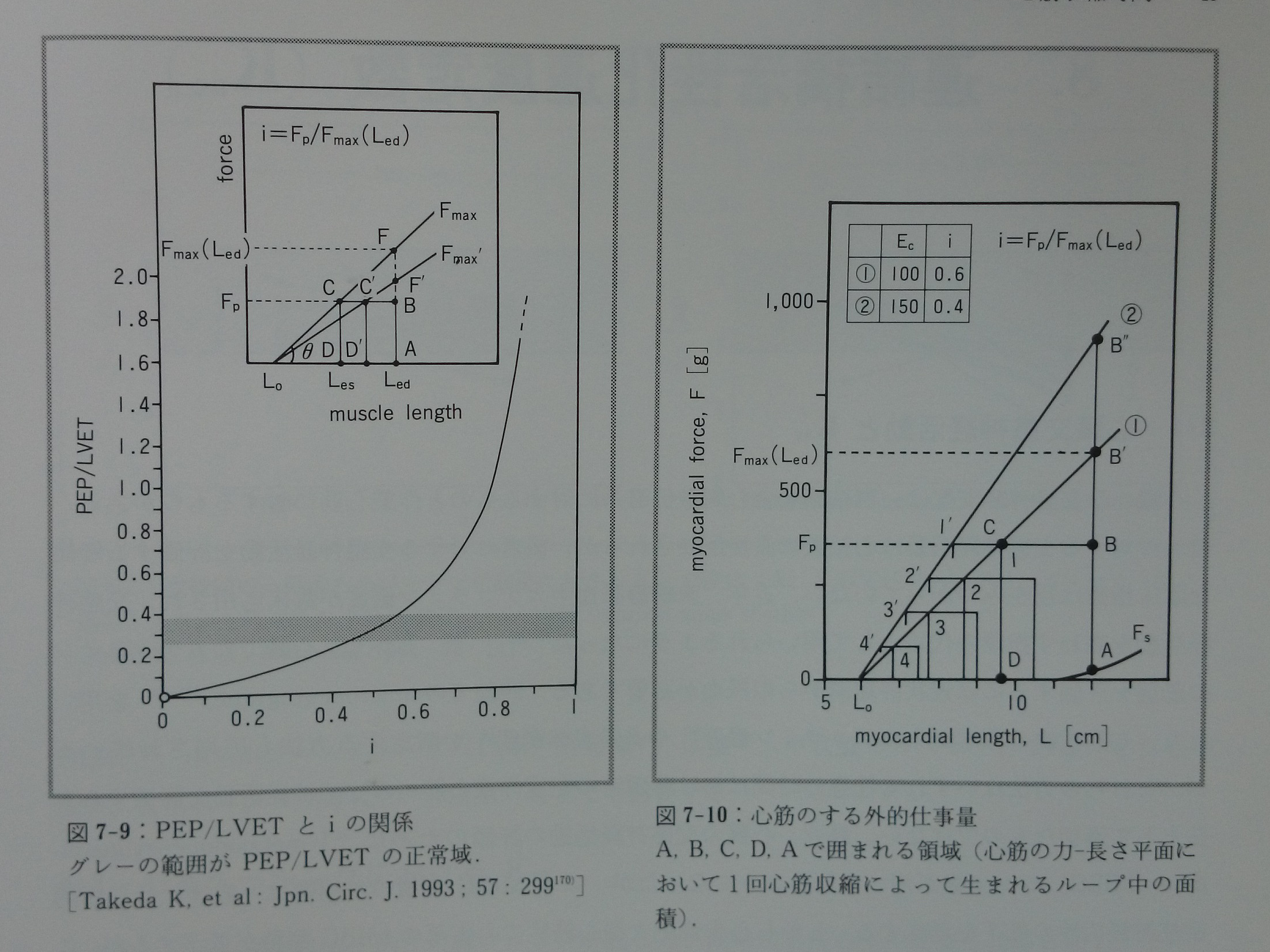
PEP/LVETは心筋収縮性を評価する一つの指標として用いられてきた206, 207)。PEP/LVETは心筋収縮性が低下すると増大し,心筋収縮性が亢進すると低値となる。そのヒトでの正常範囲は0.27から0.39である186)。モデルではこのPEP/LVETは式5-4で表現できる。PEP/LVETはiの関数である170)(図7-9)。図7-9から正常ヒトではPEP/LVETが正常範囲の時,iの値はほぼ0.5前後である。iの値は後負荷(Fp)を初期心筋長における最大心筋発生張力(Fmax(Led))で割ったものであるから(i=Fp/Fmax(Led)= Fp/[Ec(Led – Lo)]),iの値は後負荷(Fp),初期心筋長(Led),及び心筋収縮性(Ec)に依存する。図7-9の内部の図のように心筋収縮性(Ec)の低下によってiの値は大きくなる。また後負荷増大や初期心筋長の短縮によってもiは増加することがわかる。iの関数であるPEP/LVETもiと同様に後負荷,初期心筋長及び心筋収縮性に依存するので,心筋収縮性の指標としては適切ではない。
心筋のする外的仕事は心筋の力ー長さ関係平面において一回心筋収縮によって生まれるループの中の面積に相当する(図7-10)。定常状態で収縮する心筋の外的仕事量を最大にするには,理論的にはiの値が0.5となる時である。正常安静ヒトのiは約0.5であるから,生理的定常状態のヒト心臓における前負荷,後負荷,心筋収縮性の制御目標は「心筋の最大外的仕事量の達成」であると予想される。
しかし,心不全ではPEP/LVETが増大するので95, 207),iの値も増加することになる(図7-9)。従って心不全では生体にとってより重要な何か別の目標を達成するために,この「心筋の最大外的仕事量の達成」が実現できない状況にあると考えられる。この何か別のより重要な目標とは,連結橋一個のエネルギー効率を表す基本的指標である「エネルギー張力変換比率」(10章で詳述する)の改善であると予測する。なぜなら,その理由は11章の慢性心不全の心臓治療で詳しく展開するが,「エネルギー張力変換比率」を改善するにはどうしても心筋収縮性の増大をある程度犠牲にしなければならないからである。