■ ９.心筋短縮速度
9.1 Vmaxと連結橋
主に1960年代，心筋の短縮速度は心筋収縮機能の指標として注目され詳しく研究された。当時，無負荷時心筋最大短縮速度(Vmax)は心筋の初期長に無関係でありその値は心筋収縮性の変化を直接的に反映すると考えられた150)。後負荷ー短縮速度関係は有名なHillの方程式(式6-5)75)そのものであり，そのY軸切片(Vmax)は連結橋の回転速度をX軸切片(Fmax)は心筋の最大張力発生能（活性連結橋の数）を表すと考えられた。この活性連結橋の数と回転速度はそれぞれ心筋収縮性を決定する最も重要な二つの独立した基本的因子であるとされた。後負荷ー短縮速度関係はこの活性連結橋の数と回転速度を同時に評価できるものとして期待された。彼らの論理からするとVmaxは連結橋の数には影響を受けず，連結橋の回転速度にのみ支配されるので心筋長には影響されないはずである。しかし，実際にはVmaxは細胞内Ca2+濃度（これは活性連結橋の数を決定する）だけでなく心筋長（前負荷）137)によってもその値が比例的に変化することが実験的30)に，またこのモデルから理論的168)にも確認され，現在ではこの後負荷ー短縮速度関係とVmaxは心筋収縮性の評価方法として最適なものではないと見なされている。しかし心筋短縮速度は収縮性指標として直感的に理解しやすいという優れた性質を持っており，臨床においては心臓超音波検査の普及とともにＭモード心エコー図から計測されるmVcf（左室平均円周心筋短縮速度）として，現在でも心機能指標としてよく利用されている。心筋短縮速度がどの様な因子によって規定されるものであるかをモデルから説明するのは有用である。
9.2 心筋短縮速度方程式
このモデルから心筋の短縮速度(v)は式6-1，6-2として導かれる168)。
v = -Ka(L – Lo)[(Ec/α)(L – Lo)/(Fp + Fr) – 1] (6-1)
= -Ka(L -Lo)[Fmax – (Fp + Fr)]/(Fp + Fr) (6-2)
式6-1から心筋短縮速度(v)は心筋長(L)，心筋に加わる外部負荷(Fp)，心筋内に存在する内部負荷(Fr)の三つの変数によって主に決定される。KaやEcの値によっても修飾され，Loも心筋短縮速度決定に関与する。心筋短縮速度は確かに心筋の収縮性指標であるEcやKaの値に依存するので細胞内Ca2+濃度，単位連結橋の発生張力，Ca2+のトロポニンへの結合速度等の心筋収縮性を規定する因子の変化を反映すると言える。同時にまた心筋短縮速度は前負荷（心筋長）と後負荷(Fp)にも支配される。従って，心筋短縮速度は理想的な心筋収縮性の指標たり得ない。
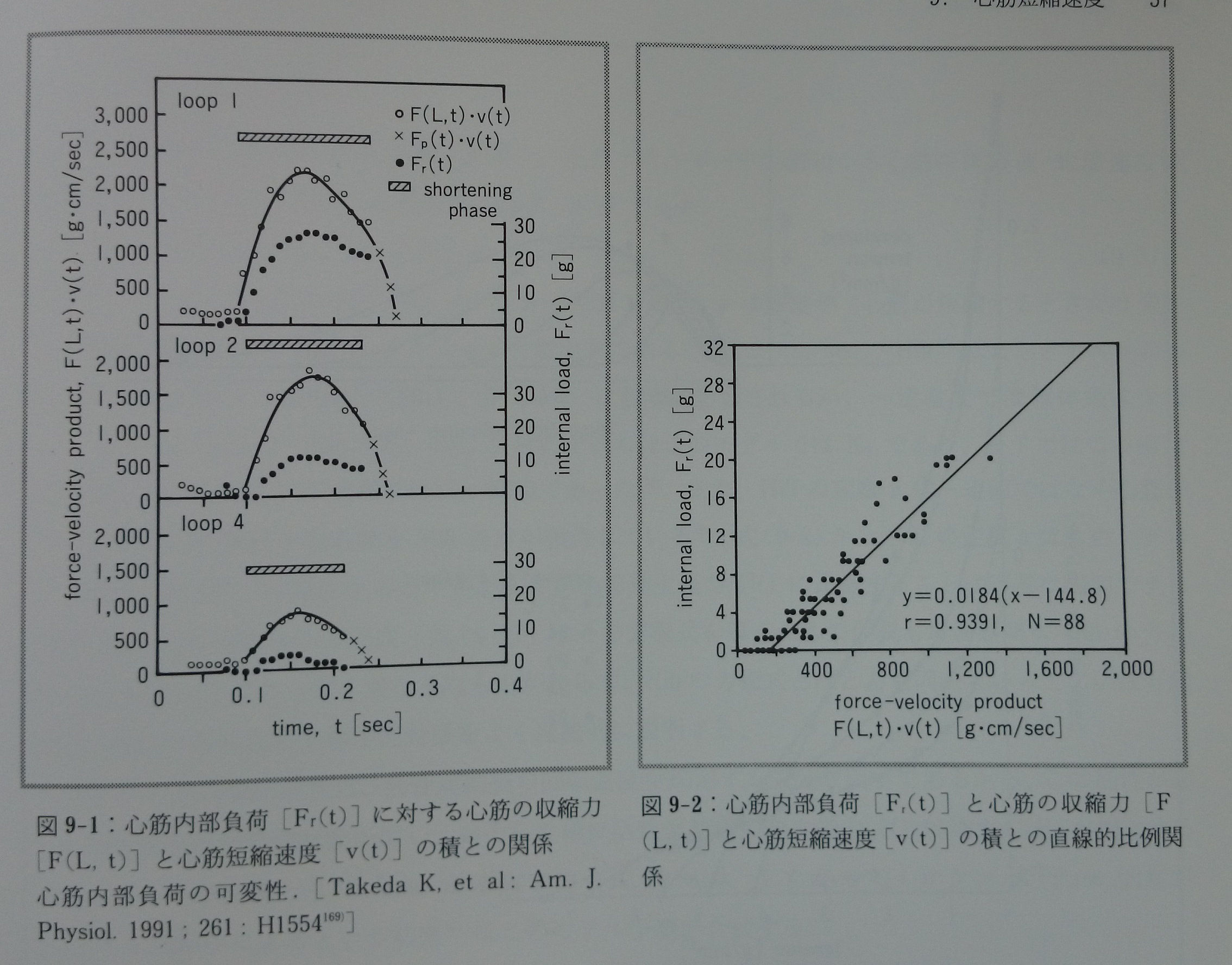
心筋短縮速度の変化の解釈を複雑にするもう一つの別の問題がある。それは心筋の内部負荷Frが心筋の収縮力Fと心筋短縮速度vの積と比例関係にあり103, 169)（図9-1，9-2），常に一定ではないことである（心筋内部負荷の可変性）。心筋短縮速度と密接に関連があり短縮熱75)の原因でもあると推測される内部負荷発生の詳細なメカニズムは不明である。もし内部負荷が一定値ならば心筋短縮速度の変化を解釈するのは易しいが，「内部負荷の可変性」の問題があるために心筋短縮速度変化の解釈は極めて困難となってしまう。
9.3 VmaxとFmax
式6-1からY軸切片(Vmax)，X軸切片(Fmax)はそれぞれ式6-3，6-4として表現される168)。
Vmax = Ka(L – Lo)[(Ec/α)(L – Lo)/Fr – 1] (6-3)
Fmax = (Ec/α)(L – Lo) (6-4)
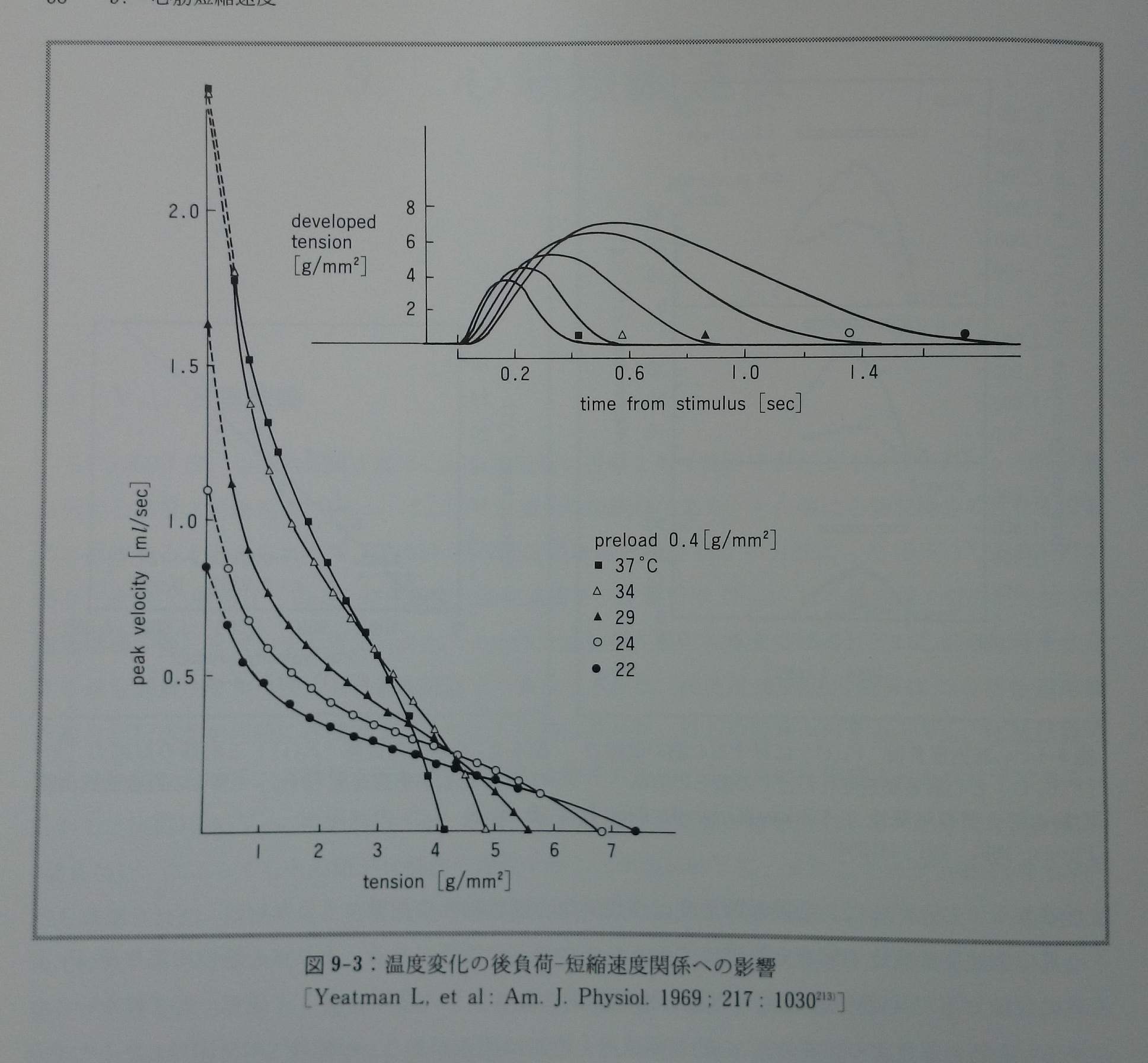
Vmaxは主にKaとEcに影響され，Fmaxは主にEcに影響される。後負荷ー短縮速度関係の実験において，心筋を37℃から24℃に冷却した時Vmaxは37℃の値の39％に減少し，Fmaxは140％に増大した213)（図9-3）。この実験のtime to peak tensionから推定したKaは37℃から24℃への冷却で37℃の値の36％に低下した。同様の冷却でのFmaxの変化率は140％であったことから，Ecの変化率は140％であると予測される。別の実験からも心筋の冷却はKaを低下させ102, 153)，Ecを増大させる58, 102, 111, 122, 153)ことが分かっている。このように冷却によるKaの低下率がEcの増加率より大きければ，心筋の冷却によってVmaxは低下し（0.36×1.40=0.50：他の条件が同じならば，予測はVmaxの50%低下となる），Fmaxは増大することがモデルから示される。この条件では同時に心筋の最大張力発生速度(dF/dtmax)や最大左室圧発生速度(LV dP/dtmax)も低下する。なぜならdF/dtmax，LV dP/dtmaxもKaとEcの積に比例し（式3-6参照），その意味でdF/dtmaxとLV dP/dtmaxはVmaxと同じ性質を持つパラメーターであるからである。37℃から24℃への冷却でdF/dtmaxは57%に低下した213)（予測はdF/dtmaxの50%低下）。このモデルの予測は後負荷ー短縮速度関係の実験事実を良く説明する。
9.4 Hillの方程式
Hillは心筋の発生する熱を正確に計測し，そのエネルギー学的解析から心筋の後負荷ー短縮速度関係を確立した。そのHillの方程式75)とは式6-5である。
v = – b(Fmax – Fp)/(Fp + a) (6-5)
記号はこのモデルに合わせてある。aとbは定数であり，aは短縮熱（心筋が短縮するときだけ発生する熱量：単位はgram）で，bはエネルギー放出率である（単位はcm/sec）。Hill75)によるとカエルの心筋標本では定数bを心筋長で除した値（b/L）は温度に影響されるが，一定温度では個体差は少なく，10℃で2.05 sec-1であった。b/Lに対応するのはこのモデルではKaであり，ヒトではこの値は36℃で7.6±0.4 sec-1で同様にほぼ一定値であった170)。また，Hillの定数aは一定値ではなく心筋の発生する張力に依存する結果をHill自身が報告している76)。式6-2からHillの定数aはこのモデルでは内部負荷(Fr)に対応するので，定数aが心筋発生張力(F)に比例することは容易に説明できる（図9-2）。このモデルの方程式（式6-2）はその方程式を導くための仮説も理論展開もHillの方程式（式6-5）とは全く異なるにもかかわらず，Hillの方程式とほとんど同一といって良いほど類似し，Hillの方程式の生物学的特徴をよく理論的に説明する。
myosin ATPase活性は，活性連結橋の回転速度を決定する主要な因子であるから，この活性が高まれば活性連結橋の回転数が増し，恐らく単位活性連結橋の発生張力(f)は増大しEcが増加するであろう。その結果としてVmaxが増大する（式6-3）。従ってmyosin ATPase活性がVmaxと比例関係にあるという結果8)はこのモデルと合致する。
図9-1：心筋内部負荷[Fr(t)]に対する心筋の収縮力[F(L, t)]と心筋短縮速度[v(t)]の積との関係。心筋内部負荷の可変性。[Takeda K, et al: Am. J. Physiol. 1991;261:H1554169)]
図9-2：心筋内部負荷[Fr(t)]と心筋の収縮力[F(L, t)]と心筋短縮速度[v(t)]の積との直線的比例関係。
図9-3：温度変化の後負荷ー短縮速度関係への影響。[Yeatman L, et al: Am. J.
Physiol. 1969;217:1030213)]
★心不全治療の原理をミステリー風に解説
慢性心不全治療の原理理論を、一般の読者にも理解し易いよう推理読み物にまとめました。ミステリースタイルの要約です。